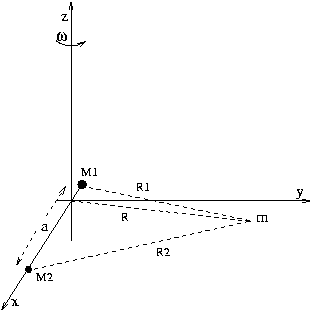
Supponiamo di avere a che fare con il Sole ed un pianeta. Poniamo che in questo sistema si presenti anche un terzo corpo di massa m molto inferiore rispetto a quella degli altri due, le cui masse, per rendere più evidente il rapporto col terzo corpo, saranno indicate rispettivamente con M1 e M2.
La condizione che ![]() e
e è essenziale perché la propria presenza
non alteri sensibilmente il centro di massa del sistema. In altre parole noi
supponiamo che i due corpi di massa maggiore interagiscano col corpo minore,
ma che quest'ultimo non agisca
sui due astri, o che i suoi effetti siano del tutto trascurabili.

Questo tipo di trattazione, che prende il nome di problema ridotto dei tre corpi, fu studiato da Lagrange nel 1772. Per affrontarlo prendiamo un sistema di riferimento non inerziale centrato nel centro di massa, con un asse solidale con i pianeti. I due astri avranno la stessa velocità angolare per cui è possibile mantenerli contemporaneamente sullo stesso asse, poniamo che sia l'asse X. Siano R1 e R2 le distanze del punto generico da M1 e M2.
Andiamo a scrivere l'energia potenziale del corpo di massa m data dalla somma di 3 contributi: i 2 potenziali gravitazionali ed il potenziale centrifugo, perché siamo in un sistema di riferimento rotante.
Si faccia attenzione che in un'eventuale derivata seconda U e avrebbero segno opposto. Andando ora a
prendere singolarmente ogni equazione, e uguagliando a zero per trovare i punti di equilibrio si ha:
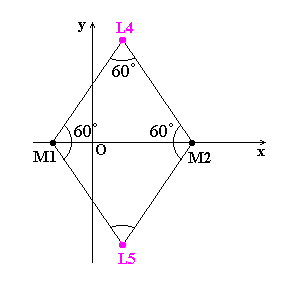 Questa, messa a
sistema con quella per z, ci dice che si hanno due soluzioni in punti
disposti a triangolo equilatero con i due corpi principali, sul piano orbitale, chiamati L4 e L5 (vedi figura a lato). Consideriamo ora la derivata lungo l'asse X; e verifichiamo che le soluzioni ora trovate soddisfino l'equazione
Questa, messa a
sistema con quella per z, ci dice che si hanno due soluzioni in punti
disposti a triangolo equilatero con i due corpi principali, sul piano orbitale, chiamati L4 e L5 (vedi figura a lato). Consideriamo ora la derivata lungo l'asse X; e verifichiamo che le soluzioni ora trovate soddisfino l'equazione Occupiamoci ora delle soluzioni
sull'asse x, cioè per y=z=0, in allineamento con i due
corpi principali. E' ovvio intanto che ci sia un punto esterno ai due corpi,
uno a destra ed uno a sinistra di entrambi. Infatti per punti
esterni le forze gravitazionali tendono a riportare la massa verso il centro,
mentre la forza centrifuga tende a portarla verso l'esterno. Poiché entrambe le
forze diminuiscono con R1 e R2 ed essendo la forza centrifuga monotòna crescente verso la periferia, certamente esisterà una configurazione di equilibrio. 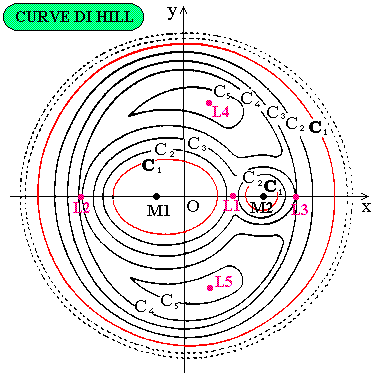
Esiste anche un terzo punto (ed uno soltanto) interno.
Risolvendo l'equazione (4) si trovano le ascisse dei tre punti Lagrangiani sull'asse X i cui valori sono stati tabulati da Plavec e Kratochvil (1964) in funzione del rapporto di massa fra i due corpi. Stabilità dei punti Lagrangiani
Abbiamo trovato cinque punti di equilibrio, le cui coordinate sono le soluzioni esatte del problema dei tre corpi ristretto, ovvero sono soluzioni statiche e stazionarie nel sistema di riferimento ruotante.
E’ ora lecito chiedersi di che natura di equilibrio si tratti, stabile (il corpo, se perturbato dalla sua posizione, comunque nel tempo tende a ritornare nel suo punto Lagrangiano) o instabile (il corpo, a seguito della perturbazione, si allontana indefinitamente dalla sua posizione).
Consideriamo dunque una soluzione di equilibrio (![]() ) e introduciamo una piccola perturbazione nella posizione cui corrisponda una perturbazione in velocità anch’essa piccola :
) e introduciamo una piccola perturbazione nella posizione cui corrisponda una perturbazione in velocità anch’essa piccola :
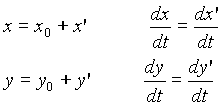
Le equazioni del moto dunque diventano :
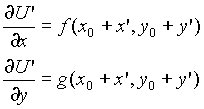
Poiché abbiamo imposto che le perturbazioni siano di piccola entità, possiamo sviluppare i secondi membri delle equazioni in serie di Taylor :
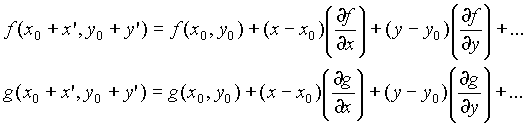
Le derivate si intendono sempre calcolate in (![]() ), il primo termine nelle equazioni è nullo in quanto rappresenta le soluzioni di equilibrio e, sia per la f che per la g, vale la seguente :
), il primo termine nelle equazioni è nullo in quanto rappresenta le soluzioni di equilibrio e, sia per la f che per la g, vale la seguente :
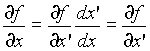
Pertanto sostituendo si ottiene :
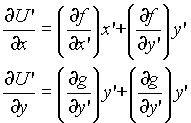
Questo, grazie alla particolare forma del potenziale, è un sistema di equazioni differenziali del 2° ordine a coefficienti costanti, la cui soluzione pertanto sarà del tipo :
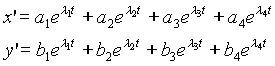
La natura di queste funzioni è strettamente legata ai coefficienti λi :
Analizzando i coefficienti per i 5 punti Lagrangiani si ottiene che i punti L1, L2, L3 sono sempre posizioni di equilibrio instabile, mentre per quel che riguarda i punti L4, L5 occorre valutare il rapporto di massa dei due corpi principali :
Se 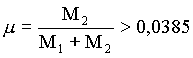 allora avremo un equilibrio instabile, come L1, L2, L3.
allora avremo un equilibrio instabile, come L1, L2, L3.
Nel sistema Sole-Giove μ<0,001 pertanto L4 ed L5 sono punti di equilibrio stabile.